代码
xxxxxxxxxxfloat Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; }背景
第一眼看代码我们可以get到这个函数需要输入一个浮点数,输出一个浮点数,那我们接下来先拆解下这个输入输出的秘密。首先,我们知道一个单位向量的公式。
出于计算机硬件设计的历史原因,硬件除法指令和开方的实现性能较差,你可以查看intel的指令手册关于latency的数据。那我们可以从软件层规避掉这种指令吗?答案是可以的,我们接下来看看id software的工程师是如何处理这个问题的。
那么我们还需要找到一个近似函数也就是Q_rsqrt替代。
到这里我们输入输出就搞明白了,输入是,输出是。
注释1: evil floating point bit level hacking
因为我们不能在浮点数上进行位运算的操作,我们先将float转成int。
xxxxxxxxxxi = * ( long * ) &y; // evil floating point bit level hacking 可以看看下面quake 2 engine的一个函数Q_fabs(float absolute)。
xxxxxxxxxx// from quake 2 code// *(TYPE*) &VAR, since we can't perform bitwise operation on float point numberfloat Q_fabs (float f){ int tmp = * ( int * ) &f; // set the sign bit // 7F => 0111 1111 tmp &= 0x7FFFFFFF; return * ( float * ) &tmp;}注释2: what the fuck
xxxxxxxxxxi = 0x5f3759df - ( i >> 1 ); // what the fuck? 第一步转换成函数等式消除除法指令。
我们需要找到一个的近似替换函数,但首先先看看如何利用二进制的数据计算浮点数,例如浮点数,我们利用十进制转二进制计算器(包含对应计算的算法步骤)转换成二进制的形式:。
标准化该二进制数字,用任意base转换公式计算十进制数值。
然后得到浮点数的计算公式。
比方说上述的,就可以写为。
转换公式(2)为方程。
,,出于某种原因是该算法的最优参数。
该公式可以近似替换为。
然后第二步我们将float类型二进制转换为int类型数值,首先先看一下float的二进制格式。

根据浮点数编码的定义。
例如相对应的值为,可以用这个在线的浮点数转换网站验证我们的结果。
于是我们可以得到如何解析浮点数二进制转换成整数的公式。
根据公式(3)得。
可以看到和的plot曲线是很近似的。
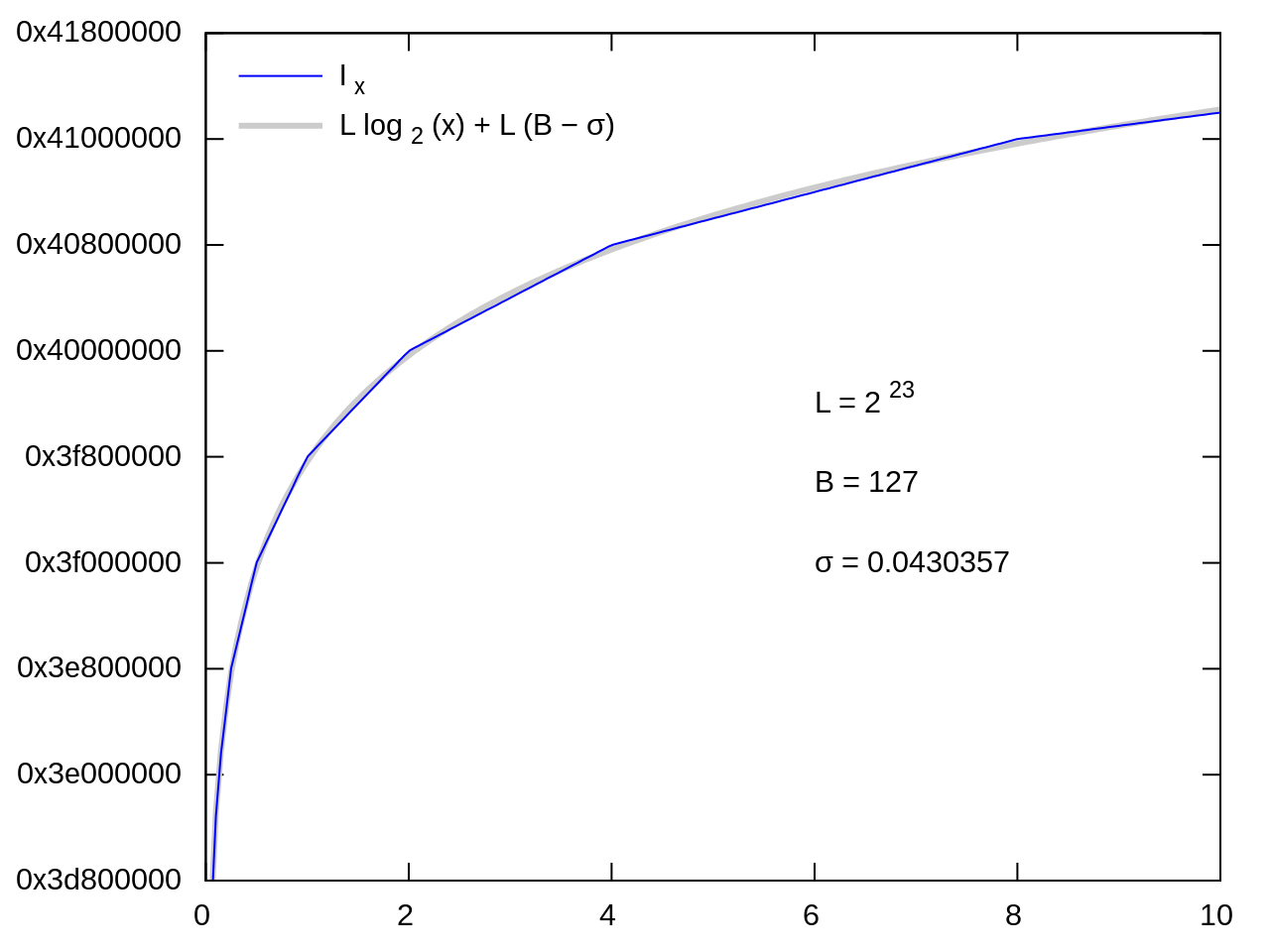
带入公式(1)得。
因为是常量,于是我们可以得到代码里的"magic number"。
xxxxxxxxxxi = 0x5f3759df - ( i >> 1 ); // what the fuck? 注释3: 1st iteration
xxxxxxxxxxy = y * ( threehalfs - ( x2 * y * y ) );Newton's method
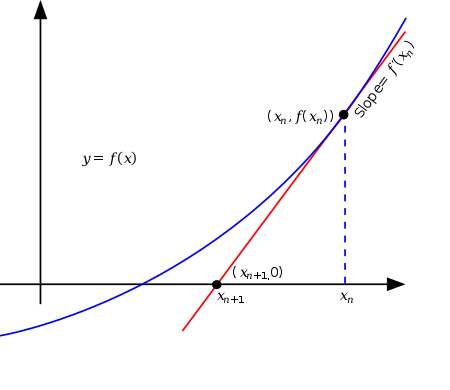
比如说。
带入公式(4)。
xxxxxxxxxxfloat sqrt_impl_by_newton_method(float x){ // initial guess float y = 0.5f * x; for (int i = 0; i < 5; i++) { y = 0.5f * (y + x / y); } return y;}回到。
带入公式(4)。
源代码的实现。
xxxxxxxxxxy = y * ( threehalfs - ( x2 * y * y ) );